Addition Of Two Matrix Algorithm
The two matrices have the same number of rows and columns. Addition Of Two Matrices Using For Loop 1 If both matrices are of the same size then only we can add the matrices.
 The 4th Grade May Niacs Multiplication Matrix Box Teaching Multiplication Multiplication Math Journals
The 4th Grade May Niacs Multiplication Matrix Box Teaching Multiplication Multiplication Math Journals
3 Read row numbercolumn number and initialize the double dimensional arrays mat1 mat2 res with same row numbercolumn number.

Addition of two matrix algorithm. We can treat each element as a row of the matrix. The program can be extended for rectangular matrices. Heres a general algorithm for adding matrices.
If the matrices dont have the same shape the addition will not be possible. Matrix addition in Python is a technique by which you can add two matrixes of the same shape. Step 2 - If the number of rows and number of columns of matrix 1 and matrix 2 are equal then execute step 3 else addition not possible Step 3 - for i1 to rowsmatrix 1 for j1 to columns matrix 1 Input matrix 1 ij Input matrix 2 ij matrix 3 ij matrix 1 ij matrix 2 ij.
In Linear Algebra the addition of two matrices is an elementary operation analogous to the addition of two numbers. Its computational complexity is therefore in a model of computation for which the scalar operations require a constant time in practice this is the case for floating point numbers but not for. Flowchart for Addition of Two Matrices.
The following post can be useful for extending this program. Step 4- Display matrix 3 ij. The matrix elements are stored in F.
The file first stores the elements of A and then those of B. Algorithm Addition of two matrices 0. At each iterationshall add the corresponding elements from two matrices and shall store the result.
DONT Check the sizes of two matrices mn and tu. In Python we can implement a matrix as nested list list inside a list. 10 10 10 10 10 10 10 10 10.
A file F holds the non-zero elements of two large nn matrices A and B. Nested for loops only to iterate through each row and columns. Addition of two matrices can be performed by adding their corresponding elements as A B ij A ij B ij.
If m t and n u then we can add them o therwise we just cant do it. If they can be added then create a new square matrix of size mn. It is important to note that matrix multiplication is not commutative.
Matrix multiplication follows distributive rule over matrix addition. It is not possible to add a 2 3 matrix with a 3 2 matrix. Moreover the addition in matrices works one way which means that the 11.
Given this precondition the sum of two. In these problem we use nested List comprehensive. Our task is to display the addition of two matrix.
A B C AB AC Right Distribution A B C AC AC. Enter the values of first matrix of size 1 2 3 4 5 6 7 8 9 enter the values of second matrix 9 8 7 6 5 4 3 2 1 addition of two matrix. For each element in A find the element at the same.
At each point we add the corresponding elements in the two matrices and store it in the result. The only imposed condition is that the two matrices you are summing must have the same dimensions. When a matrix is multiplied on the right by a identity matrix the output matrix would be same as matrix.
Matrix addition The following Flowchart represents the addition of two matrices. Suppose we multiply two matrices and of the same order then. Two matrices A and B can be added if and only if they have same dimensions that are the same number of rows and columns.
2 Use the double dimensional array to store the matrix elements. The matrix entries are stored as triplets ijvalue where value is the ijth element of a matrix. Given two user input matrix.
When two matrices are of order m x p and n x m the order of product will be n x p. This property is called multiplicative identity. START Step 1 - Input matrix 1 and matrix 2.
Using nested list comprehension. This is the general case. For example say matrix A is of the order then the matrix B can be added to matrix A if the order of B is also.
Consider two matrices A B. These matrices can be added iff if and only if the order of the matrices are equal ie. Result matrix is 2 2 2 2 4 4 4 4 6 6 6 6 8 8 8 8.
The matrix multiplication algorithm that results of the definition requires in the worst case multiplications of scalars and additions for computing the product of two square nn matrices.
 Operation Of Matrices Matrix Commutative Operator
Operation Of Matrices Matrix Commutative Operator
 Bubble Sort Using Java Program Sorting An Array Of Int Using Bubblesort Bubble Sort Algorithm Bubble Sort Java
Bubble Sort Using Java Program Sorting An Array Of Int Using Bubblesort Bubble Sort Algorithm Bubble Sort Java
 Adding Two Polynomials Using Linked List Geeksforgeeks
Adding Two Polynomials Using Linked List Geeksforgeeks
 Matrix Multiplication Using Operator Overloading In Cpp Computer Aided Matrix Multiplication Multiplication Matrix
Matrix Multiplication Using Operator Overloading In Cpp Computer Aided Matrix Multiplication Multiplication Matrix
![]() Subset Sum Backtracking 4 Geeksforgeeks
Subset Sum Backtracking 4 Geeksforgeeks
 Flowcharts With Examples And Explanation Of Symbols Easycodebook Com Flow Chart Program Flowchart Programming Tutorial
Flowcharts With Examples And Explanation Of Symbols Easycodebook Com Flow Chart Program Flowchart Programming Tutorial
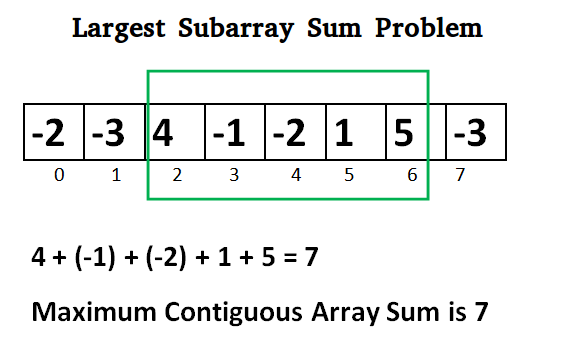 Largest Sum Contiguous Subarray Geeksforgeeks
Largest Sum Contiguous Subarray Geeksforgeeks
 Backpropagation Algorithm This Or That Questions Algorithm Tapestry
Backpropagation Algorithm This Or That Questions Algorithm Tapestry
 Euclidean Algorithm To Calculate Gcd In Python Algorithm Python Calculator
Euclidean Algorithm To Calculate Gcd In Python Algorithm Python Calculator
 We Finally Began 2 Digit By 2 Digit Multiplication This Week The Kids Are Absolutely Loving The Matrix Box We Use To I Math Multiplication Math Multiplication
We Finally Began 2 Digit By 2 Digit Multiplication This Week The Kids Are Absolutely Loving The Matrix Box We Use To I Math Multiplication Math Multiplication
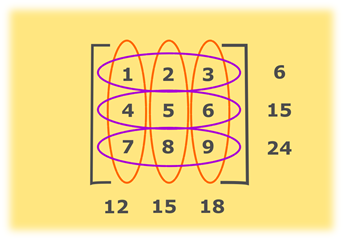 Program To Find The Sum Of Each Row And Each Column Of A Matrix Javatpoint
Program To Find The Sum Of Each Row And Each Column Of A Matrix Javatpoint
 Pin By Michelle Moore On 5th Grade Anchor Charts Math Charts Elementary Math Classroom Math Classroom
Pin By Michelle Moore On 5th Grade Anchor Charts Math Charts Elementary Math Classroom Math Classroom
 In This C Program You Will Learn C Program To Add Two Numbers And Also Learn Program To Add Two Numbers In C Using Function Third Learn C Algorithm Programming
In This C Program You Will Learn C Program To Add Two Numbers And Also Learn Program To Add Two Numbers In C Using Function Third Learn C Algorithm Programming
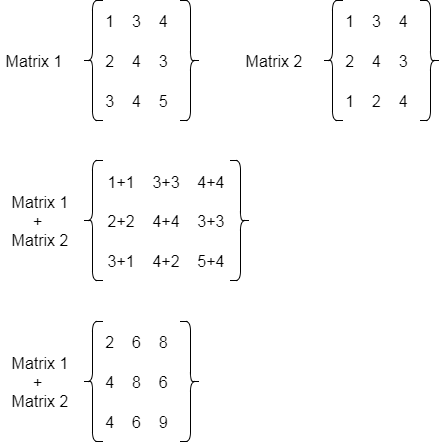 Java Program To Add 2 Matrices Javatpoint
Java Program To Add 2 Matrices Javatpoint
 Java Biginteger Arithmetic Arithmetic Subtraction Coding
Java Biginteger Arithmetic Arithmetic Subtraction Coding
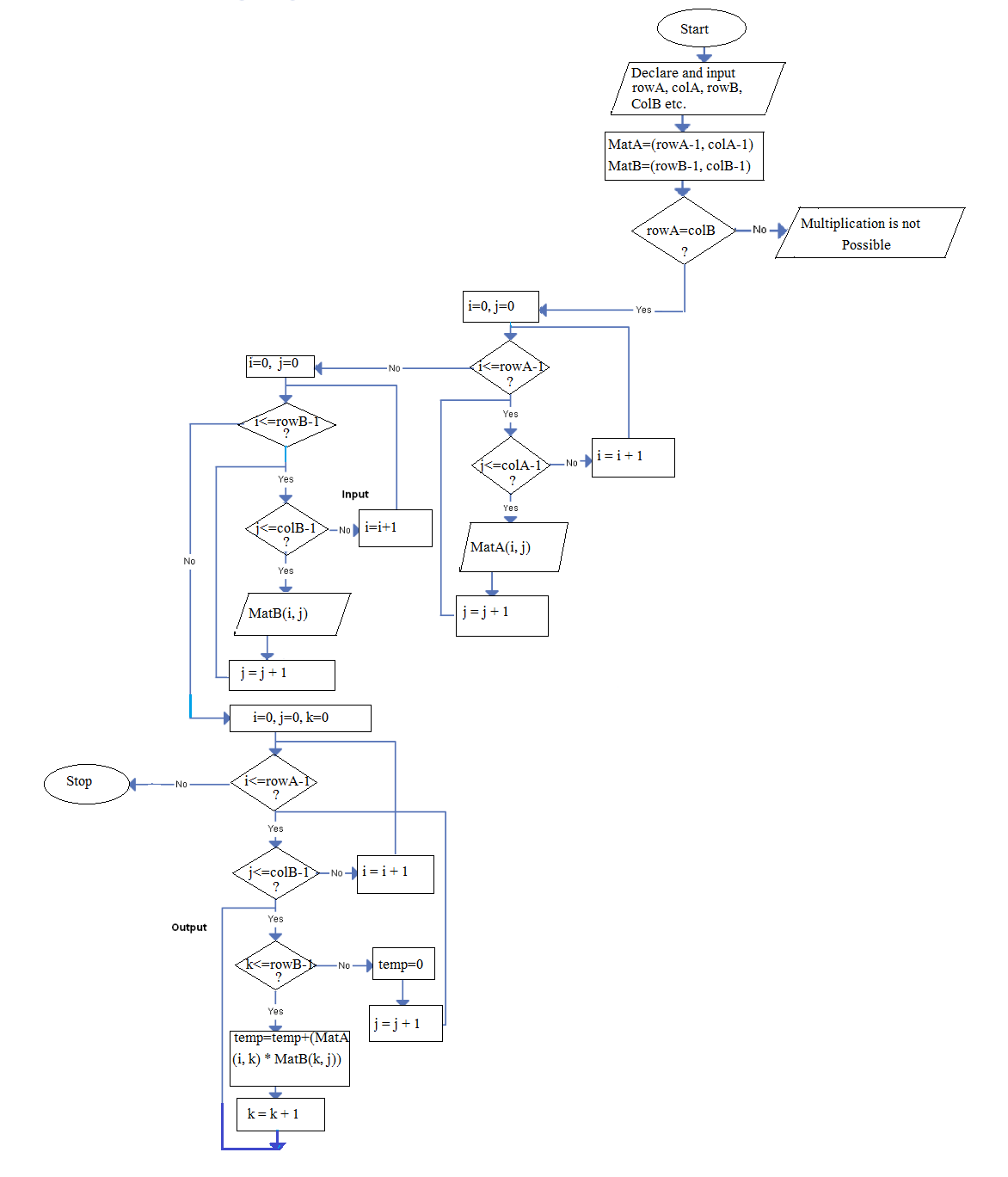 Matrix Multiplication Algorithm And Flowchart Code With C
Matrix Multiplication Algorithm And Flowchart Code With C
 Rigor Have You Tried Capacity Matrices Use This Template To Create A Checklist Of Standards For Personalized Learning Student Centered Learning Metacognition
Rigor Have You Tried Capacity Matrices Use This Template To Create A Checklist Of Standards For Personalized Learning Student Centered Learning Metacognition
 Inverse Of A Matrix Matrix Commutative Abs
Inverse Of A Matrix Matrix Commutative Abs
